Answer:
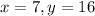
Explanation:
The tick marks you see on the sides denote congruence. If they have the same number of tick marks, then their side length are congruent.
And, recall that congruent side lengths have the same measure.
So, look at the sides with 2 tick marks. They are congruent. Therefore:
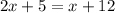
Subtract x from both sides:
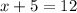
Subtract 5 from both sides:
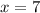
So, x is 7.
Now, look at the sides with only 1 tick mark. Again, they are congruent. Thus:
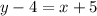
We already know x is 7. So:
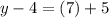
Add:
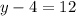
Add 4 to both sides:

So, y is 16.