Question

point A B and C are collinear on AC and AB:BC = 3/4. A is located at (x,y), B is located at (4,1) and C is located at (12,5). what are the values of x and y?

Answer 1

x = -2 and y = -2

Explanation:

The expression for calculating the point that divides the coordinate of two endpoints A(x, y) and B (x₁, y₁) in the ratio a:b with point C(X, Y) on the line is as shown below;

`B`
`(X, Y) =`
`((ax_1+bx)/(b+a), (ay_1+by)/(b+a))`

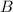
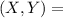
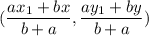
Given B(X, Y) = (4, 1), C(x₁, y₁) = (12,5) and AB:BC = a:b = 3/4

From the given coordinates, X = 4, Y = 1, x₁ = 12 y₁ = 5, a = 3 and b =4

From the coordinates above;

`X = (ax_1+bx)/(b+a)`

`4 = (3(12)+4x)/(4+3)\\\\4 = (36+4x)/(7)\\\\\\4*7 = 36+4x\\28 = 36+4x\\28-36 = 4x\\-8 = 4x\\x = -8/4\\x= -2`

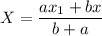
Similarly to get y;

`1 = (3(5)+4y)/(4+3)\\\\1 = (15+4y)/(7)\\\\\\1*7 = 15+4y\\7 = 15+4y\\7-15 = 4y\\-8 = 4y\\y= -8/4\\y= -2`

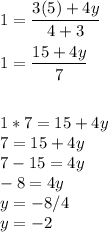
Hence the value of x is -2 and y is -2.