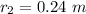Answer:
The distance is
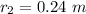
Step-by-step explanation:
From the question we are told that
The distance from the conversation is
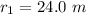
The intensity of the sound at your position is
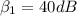
The intensity at the sound at the new position is

Generally the intensity in decibel is is mathematically represented as
![\beta = 10dB log_(10)[(d)/(d_o) ]](https://img.qammunity.org/2021/formulas/physics/college/xsjpc9ovj2ygdunxoy1q5bud8yr7z8xjqp.png)
The intensity is also mathematically represented as
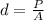
So
![\beta = 10dB * log_(10)[(P)/(A* d_o) ]](https://img.qammunity.org/2021/formulas/physics/college/bv7c37h0a2n0yrbti7qladhthk8luyr9w5.png)
=>
![(\beta)/(10) = log_(10) [(P)/(A (l_o)) ]](https://img.qammunity.org/2021/formulas/physics/college/zj3qhcp72rpqg5i53psw5wmplk80q5u9s6.png)
From the logarithm definition
=>
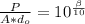
=>
![P = A (d_o ) [10^{(\beta )/( 10) } ]](https://img.qammunity.org/2021/formulas/physics/college/bzvutosoi4f0fppzorixupnyw5j95dmcoy.png)
Here P is the power of the sound wave
and A is the cross-sectional area of the sound wave which is generally in spherical form
Now the power of the sound wave at the first position is mathematically represented as
![P_1 = A_1 (d_o ) [10^{(\beta_1 )/( 10) } ]](https://img.qammunity.org/2021/formulas/physics/college/ggjglyhoy27v7mwt9ujr42fkhweby9gvpc.png)
Now the power of the sound wave at the second position is mathematically represented as
![P_2 = A_2 (d_o ) [10^{(\beta_2 )/( 10) } ]](https://img.qammunity.org/2021/formulas/physics/college/dhw8dpfvxakvqmk680mbct723d4ml9ol15.png)
Generally power of the wave is constant at both positions so
![A_1 (d_o ) [10^{(\beta_1 )/( 10) } ] = A_2 (d_o ) [10^{(\beta_2 )/( 10) } ]](https://img.qammunity.org/2021/formulas/physics/college/yen7jsc1kc17maabdks76ta5fnay2f7udi.png)
![4 \pi r_1 ^2 [10^{(\beta_1 )/( 10) } ] = 4 \pi r_2 ^2 [10^{(\beta_2 )/( 10) } ]](https://img.qammunity.org/2021/formulas/physics/college/h21jkrw9sr5v08yhkmx4qsdyz74dm55ivy.png)
![r_2 = \sqrt{r_1 ^2 [\frac{10^{(\beta_1)/(10) }}{ 10^{(\beta_2)/(10) }} ]}](https://img.qammunity.org/2021/formulas/physics/college/smbp25exhqm8ao030fl56lgfs23mn8iiy6.png)
substituting value
![r_2 = \sqrt{ 24^2 [\frac{10^{( 40)/(10) }}{10^{(80)/(10) }} ]}](https://img.qammunity.org/2021/formulas/physics/college/poh2hnqvvrpr9722jiv4nlrd0zpgw1n2i3.png)