Question

Which of the following statements is/are correct?

A. The instantaneous speed is always equal to the magnitude of instantaneous velocity.
B. The average speed is always equal to the magnitude of average velocity.
C. Neither of these statements is correct.
D. Both of these statements are correct.

Answer 1

The correct answer is:

The instantaneous speed is always equal to the magnitude of instantaneous velocity. (A)

Step-by-step explanation:

Speed is the ratio of distance travelled to time. It is a scalar quantity.

Velocity is the rate of change of displacement with time. It is a scalar quantity, having both magnitude and direction

Instantaneous velocity is the rate of change of position for a very small time interval (at a particular point in time), while the instantaneous speed at any given time, is the magnitude of instantaneous velocity. Note that the velocity has both magnitude and direction, so at a particular point in time, the magnitude part of velocity is the same as the speed.

The formula of instantaneous velocity is:
`V_(i)=\lim_(\Delta t\rightarrow 0)(ds)/(dt)`

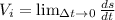
The formula of instantaneous speed is:
`Speed_((i))=(ds)/(dt)`

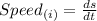
On the other hand, average speed does not equal the magnitude of average velocity, because velocity depends on displacement while speed depends on distance, and if an object in motion changes direction at any point in the motion, the velocity reduces because the angle of change in the direction will be considered, hence the speed will be greater than the velocity, therefore, the average speed is not the same as the magnitude of average velocity.