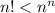Answer:
Explanation:
Hello,
We will prove it by induction.
Step 1 - for n=2
2!=2*1=2
2^2=4
and 2 < 4 so this is true for n=2
Step2 - We assume that this is true for k and we have to prove it for k+1.
Induction hypothesis is
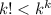
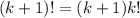
We use the induction hypothesis and we we can write that
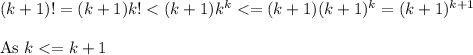
so, we prove it for k+1
Step 3- conclusion
for n >= 2 we just proved that