Question

Find the center of this circle by completing the square. x^2+y^2-6x+8y+10=0
Show work

Answer 1

Center: (3, - 4)

Explanation:

We can start to solve this problem by converting this equation into standard form. In other words, by completing the square --- (1)

Subtract " 10 " from either side of the equation x² + y² - 6x + 8y + 10 = 0

x² + y² - 6x + 8y = - 10

Step 1: Complete the square for the expression " x² - 6x "

Using the quadratic equation ax² + bx + c we know that a = 1, b = - 6, c = 0. Assume that d = b / 2a. We have...

d = - 6 / 2(1) = - 6 / 2 = - 3

Now let's assume that e = c - (b²) / 4a...

e = 0 - (-6)² / 4(1) = 0 - 36 / 4 = 0 - 9 = 9 (Substitute values d and e)

(x - 3)² - 9

Step 2: Respectively we can complete the square for the remaining expression " y² + 8y "

Here a = 1, b = 8, c = 0

d = 8 / 2(1) = 8 / 2 = 4

e = 0 - (8)² / 4(1) = 0 - 64 / 4 = 0 - 16 = - 16 (Substitute values)

(y + 4)² - 16

This leaves us with the expression " (x - 3)² - 9 + (y + 4)² - 16 = - 10. " If we simplify this a bit further it leaves us with the following circle equation. Using this we can identify the center of the circle as well --- (2)

`\mathrm{Standard}\:\mathrm{Circle}\:\mathrm{Equation} : (x - 3)^2 + (y +4)^2 = 15,\\\mathrm{General}\:\mathrm{Form} : (x - h)^2 + (y +k)^2 = r^2,\\\mathrm{Properties} : \mathrm{Center} = (3, - 4), \mathrm{Radius} = √(15)`

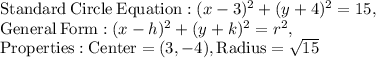
As you can see our center here is (3, - 4)