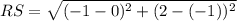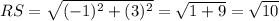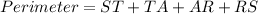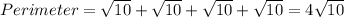Question

Find the perimeter of rhombus star

Answer 1

`4√(10)`

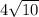
Explanation:

Perimeter of the rhombus, STAR, is the sum of the length of all it's 4 sides.

The coordinates of its vertices are given as,

S(-1, 2)

T(2, 3)

A(3, 0)

R(0, -1)

Length of each side can be calculated using the distance formula given as
`d = √(x_2 - x_1)^2 + (y_2 - y_1)^2)`

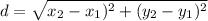
Find the length of each side ST, TA, AR, RS, using the above formula by plugging in the coordinate values (x, y) of each vertices.

`ST = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

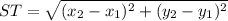
S(-1, 2) => (x1, y1)

T(2, 3) => (x2, y2)

`ST = √((2 -(-1))^2 + (3 - 2)^2)`

`ST = √((3)^2 + (1)^2) = √(9 + 1) = √(10)`

`TA = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

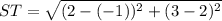
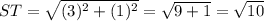
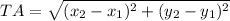
T(2, 3) => (x1, y1)

A(3, 0) => (x2, y2)

`TA = √((3 - 2)^2 + (0 - 3)^2)`

`TA = √((1)^2 + (-3)^2) = √(1 + 9) = √(10)`

`AR = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

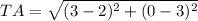
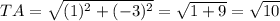
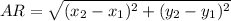
A(3, 0) => (x1, y1)

R(0, -1) => (x2, y2)

`AR = √((0 - 3)^2 + (-1 - 0)^2)`

`AR = √((-3)^2 + (-1)^2) = √(9 + 1) = √(10)`

`RS = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

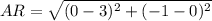
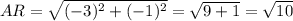
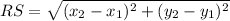
R(0, -1) => (x1, y1)

S(-1, 2) => (x2, y2)

`RS = √((-1 - 0)^2 + (2 -(-1))^2)`

`RS = √((-1)^2 + (3)^2) = √(1 + 9) = √(10)`

`Perimeter = ST + TA + AR + RS`

`Perimeter = √(10) + √(10) + √(10) + √(10) = 4√(10)`