Question

Help pls. Find the value of x.

Answer 1

Answer: x = 15 degree

Step-by-step explanation:

(x + 30) + 100 + (3x - 10) = 180 (straight angle)

x + 30 + 100 + 3x - 10 = 180
4x + 120 = 180
4x = 180 - 120
4x = 60
x = 60/4
x = 15 degree

Therefore, x = 15 degree

Answer 2

`\boxed{ \bold{ \huge{ \boxed{ \sf{x = 15 °}}}}}`

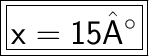
Step-by-step explanation:

`\sf{x + 30 ° + 100 ° + 3x - 10 ° = 180 °}`

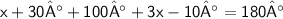
( Sum of angle in straight line )

Collect like terms

⇒
`\sf{4x + 30 ° + 100 ° - 10 ° = 180 °}`

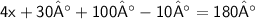
Calculate the sum or difference

⇒
`\sf{4x + 120 ° = 180 °}`

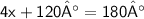
Move 120 to right hand side hand change it's sign

⇒
`\sf{4x = 180 ° - 120 °}`

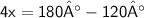
Subtract 120 from 180

⇒
`\sf{4x = 60 ° }`

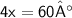
Divide both sides of the equation by 4

⇒
`\sf{ (4x)/(4) = (60)/(4) }`

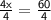
Calculate

⇒
`\sf{x = 15  °}`

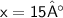
Hope I helped!

Best regards!!