Question

In the given figure, ABCD is a rectangle. Its diagonals meet at O. If OC = 3x – 4, OB = x + 4, then find OB, OC, OA, AC, BD and OD​

Answer 1

OB = 8

OC = 8

OA = 8

AC = 16

BD = 16

OD = 8

Explanation:

Given, rectangle ABCD, with diagonals AC and BD, and OC = 3x – 4, OB = x + 4,

thus, since diagonals of a rectangle are equal, therefore, AC = BD.

Invariably, 2*OC = 2*OB

Thus,
`2(3x - 4) = 2(x + 4)`

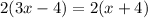
Solve for x

`6x - 8 = 2x + 8`

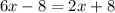
Add 8 to both sides

`6x - 8 + 8 = 2x + 8 + 8`

`6x = 2x + 16`

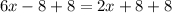
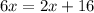
Subtract 2x from both sides

`6x - 2x = 2x + 16 - 2x`

`4x = 16`

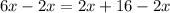
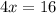
Divide both sides by 4

`(4x)/(4) = (16)/(4)`

`x = 4`

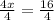
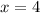
OB = x + 4 = 4 + 4 = 8

OC = 3x - 4 = 3(4) - 4 = 12 - 4 = 8

OA = OC = 8

AC = 2*OC = 2*8 = 16

BD = 2*OB = 2*8 = 16

OD = OB = 8