Answer:
x=15
Explanation:
We are given the equation:
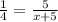
We want to solve for x. Therefore, we must isolate x on one side of the equation.
Let's begin by cross multiplying. Multiply the numerator of the first fraction by the denominator of the second. Then, multiply the denominator of the first by the numerator of the second.
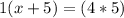
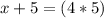
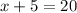
5 is being added to x. The inverse of addition is subtraction, so subtract 5 from both sides of the equation.
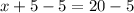
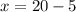
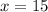
Let's check our solution. Plug 15 in for x.
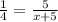

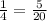
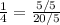

Our solution checks out, so we know it is correct.
The solution to this equation is x=15