Answer:
The current through the inductor at the end of 2.60s is 9.7 mA.
Step-by-step explanation:
Given;
emf of the inductor, V = 41.0 mV
inductance of the inductor, L = 13 H
initial current in the inductor, I₀ = 1.5 mA
change in time, Δt = 2.6 s
The emf of the inductor is given by;
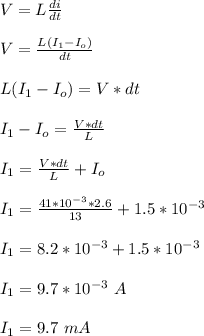
Therefore, the current through the inductor at the end of 2.60 s is 9.7 mA.