Question

) A company determines that its marginal revenue per day is given by R'(t) = 100et , R(0) = 0, where R(t) = the revenue, in dollars, on the tth day. The company's marginal cost per day is given by C'(t) = 140 - 0.3t, C(0) = 0, where C(t) = the cost, in dollars, on the tth day. Find the total profit from t = 0 to t = 5 (the first 5 days). Round to the nearest dollar. Note: P(T) = R(T) - C(T) = T 0 ∫ [R'(t) - C'(t)] dt.

Answer 1

$14038

Step-by-step explanation:

The company has marginal revenue R'(t) =
`100e^t`. Therefore its revenue R(t) is given as;

R(t) = ∫R'(t)

R(t)= ∫
`100e^t` dt =
`100e^t` + c

R(t) =
`100e^t` + c

But R(0) = 0, therefore:

R(0) =
`100e^0` + c = 0

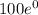`100e^0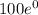` + c = 0

100 + c =0

c = -100

Also the marginal cost per day is given by C'(t) = 140 - 0.3t

C'(t) = 140 - 0.3t

C(t) = ∫C(t) = ∫ (140 - 0.3t) dt = 140t - (0.3/2) t² + C

But C(0) = 0

C(0) = 140 (0) - (0.3/2)(0)² + c = 0

c = 0

C(0) = 140t - (0.3/2) t²

Profit P(t) = R(T) - C(T) , hence the total profit from t = 0 to t = 5 is given as:

P(t) =
`\int\limits^0_5 {[R'(t)-C'(t)]} \, dt =\int\limits^0_5 {([100e^t-(140-0.3t)]} \, dt=\int\limits^0_5 {100e^t} \, dt +\int\limits^0_5 {-0.3t} \, dt +\int\limits^0_5 {-140} \, dt \\\\=[100e^t]_0^5+[ -140t]_0^5+[-0.3t^2/2]_0^5=[14841.316-100]+[-700]+[-3.75]=14038`

The profit is $14038