Answer:
a = 0
b =
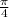
c = 0
d = 3
e = 5
f =

Explanation:
Equation of the solid sphere = x^2 + y^2 + z^2 ≤ 34 ------- (1)
at Z = 5
since the bottom of the sphere(z) is flat = 5 we will use cylindrical coordinates
concentrating in the first octant as mentioned in the question
at Z = 5 , equation 1 becomes :
x^2 + y^2 + 25 ≤ 34 = x^2 + y^2 = 9
hence the radius around the xy axis =
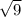 = 3
= 3
that means the radius is : 0 ≤ r ≤ 4 , 0 ≤ ∅ ≤
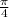
next we have to find the upper bound of: Z = ±
 we will pick out only the positive
we will pick out only the positive
5 ≤ z ≤
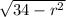
therefore for the Volume = ∫ba∫dc∫fe
a = 0
b =
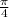
c = 0
d = 3
e = 5
f =
