Question

Determine the domain of the function (fog)(x) where f(x)=3x-1/x-4 and g(x)=x+1/x

Answer 1

Answer: (-∞,-1) ∪ (0,+∞)

Step-by-step explanation: The representation fog(x) is a representation of composite function, meaning one depends on the other.

In this case, fog(x) means:

fog(x) = f(g(x))

fog(x) =
`3(x+(1)/(x) )-(1)/(x+(1)/(x) ) -4`

`fog(x)=3x+(3)/(x) -(1)/((x^(2)+x)/(x) ) -4`

`fog(x)=3x+(3)/(x) -(x)/(x^(2)+x) -4`

`fog(x)=(3x^(2)(x^(2)+x)+3(x^(2)+x)-x-4x(x^(2)+x))/(x(x^(2)+x))`

`fog(x)=(3x^(4)+3x^(3)+3x^(2)+3x-x-4x^(3)+4x^(2))/(x(x^(2)+x))`

`fog(x)=(3x^(4)-x^(3)-x^(2)+2x)/(x(x^(2)+x))`

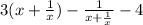
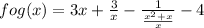
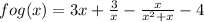
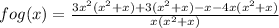
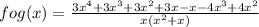
This is the function fog(x).

The domain of a function is all the values the independent variable can assume.

For fog(x), denominator can be zero, so:

`x(x^(2)+x) \\eq 0`

If x = 0, the function doesn't exist.

`x^(2)+x \\eq0`

`x(x+1) \\eq0`

`x+1\\eq0`

`x\\eq-1`

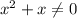
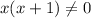
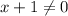
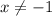
Therefore, the domain of this function is: -∞ < -1 or x > 0