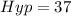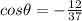Answer:
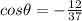
Explanation:
Given

Quadrant: 3rd
Required
Determine

This question will be solved using the Pythagoras theorem
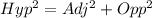
The tangent of an angle is calculated as thus;
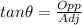
Comparing
 to
to
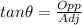
We can conclude that
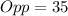
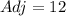
Substitute these values in the Pythagoras formula
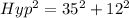
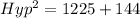
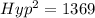
Square root of both sides

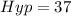
SInce
 is in the 3rd quadrant, then
is in the 3rd quadrant, then
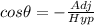
Where
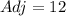 and
and