Answer:
See below.
Explanation:
4)
So we have the expression:
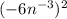
We can use the power of a product property, where:
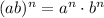
So:
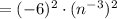
For the left, -6 squared is the same as -6 times -6. This equals positive 36.
For the right, we can use the power of a power property. The property says that:
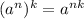
So:
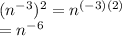
So, all together, we have:

6)
We have the expression:
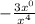
First, note that anything to the zeroth power (except for 0) is 1, thus, x^0 is also 1. Simplify:
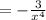
And that's the simplest we can do :)
Notes for 6)
We can put the x^4 to the numerator. Recall that when you put an exponent to opposite side, you put a negative. In other words:
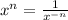
And vice versa:
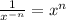
So, we can write the above as:
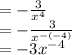
However, traditionally, we want only positive exponents, so this wouldn't be correct.