Question

Find the area of the triangle ABC A(-6,2) B(3,2) c(-2,6) D (-2,2)

Answer 1

18

Explanation:

Answer 2

18 square units.

Explanation:

Area of the triangle = ½*AB*CD

First of all, find the length of AB and CD using the distance formula,
`d = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

`AB = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

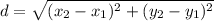
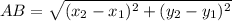
A(-6, 2) => (x1, y1)

B(3, 2) => (x2, y2)

`AB = √((3 -(-6))^2 + (2 - 2)^2)`

`AB = √((9)^2 + (0)^2) = √(81) = 9`

`CD = √((x_2 - x_1)^2 + (y_2 - y_1)^2)`

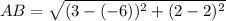
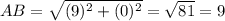
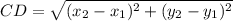
C(-2, 6) => (x1, y1)

D(-2, 2) => (x2, y2)

`CD = √((-2 -(-2))^2 + (2 - 6)^2)`

`CD = √((0)^2 + (-4)^2) = √(16) = 4`

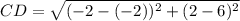
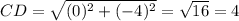
AB = 9

CD = 4

Area of rectangle = ½*AB*CD = ½*9*4 = 9*2 = 18 square units.