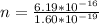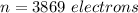Answer:
a
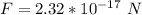
b
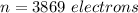
Step-by-step explanation:
From the question we are told that
The charge on each water drop is
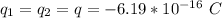
The distance of separation is
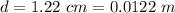
Generally the electrostatic force between the water drops is mathematically represented as
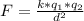
Here k is the coulombs constant with value
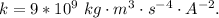
So
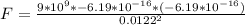
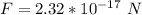
Generally the quantity of charge is mathematically represented as
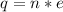
Here n is the number of electron present
and e is the charge on one electron with value

So