Answer:
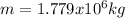
Step-by-step explanation:
Hello,
In this case, mass and volume define density as shown below:
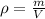
Whereas the mass is computed by:
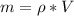
Thus, knowing the dimensions of the pool, we compute its volume:
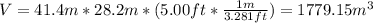
But in cubic centimetres:
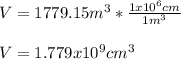
Therefore, the mass in kilograms turns out:
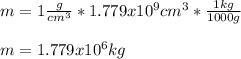
Regards.