Question

if a right cylinder have the same radius and height as the oblique cylinder shown here, what is the volume of the right cylinder? Use 3.14 for pi. Round to the nearest whole number.​

Answer 1

`\displaystyle V_\text{right} \approx 1696\text{ units}^3`

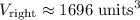
Explanation:

Recall that the volume for an oblique cylinder is the same for the volume of a right cylinder. That is:

`\displaystyle V_\text{right} = V_\text{oblique} = \pi r^2h`

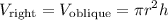
Hence, find the volume of the oblique cylinder:

`\displaystyle \begin{aligned} V_\text{oblique} & = (3.14)(6)^2(15) \\ \\ & = 1695.6 \text{ units}^3 \\ \\ &\approx 1696\text{ units}^3\end{aligned}`

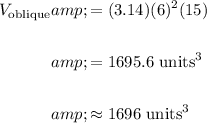
Therefore:

`\displaystyle V_\text{right} \approx 1696\text{ units}^3`

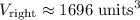
In conclusion, the volume of the right cylinder is about 1696 units³.