Answer:
![\lim_(x\to3^-)\sin{(\pi)/(\floor[x])=1](https://img.qammunity.org/2021/formulas/mathematics/high-school/s4nzkuq4axu2pfs8txb3pw272vties1xpx.png)
![\lim_(x\to3^+)\sin{(\pi)/(\floor[x])=(\sqrt3)/(2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/yvdijn186wfr99n8wr0crntno8njxivxts.png)
![\lim_(x\to3)\sin{(\pi)/(\floor[x])=(\sqrt3)/(2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/s7njy7ue34la0s7fzbsrelwgjny85j0my1.png)
Explanation:
So we want to left and right hand limits of the function:
![f(x)=\sin{(\pi)/(\floor[x])](https://img.qammunity.org/2021/formulas/mathematics/high-school/lvfw20h44vv8jnswfa0mnlihrwmtm84ivh.png)
as x approaches 3.
Note that the [x] means the floor function a.k.a the greatest integer function. In other words, the value of the function will be the greatest integer less than or equal to x.
1) Left
So we have the limit:
![\lim_(x\to3^-)\sin{(\pi)/(\floor[x])](https://img.qammunity.org/2021/formulas/mathematics/high-school/miiv5ceq2ln4qkuopqveh0hpujefilw1ke.png)
Note that since we're coming from the left, the values are 2.9, 2.99, and 2.999...
As I mentioned previously, the floor function outputs the greatest integer less than or equal to x.
With 2.9, 2.99, and 2.999, the greatest integer less than or equal to x is 2.
Therefore:
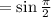
Simplify:
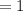
So:
![\lim_(x\to3^-)\sin{(\pi)/(\floor[x])=1](https://img.qammunity.org/2021/formulas/mathematics/high-school/s4nzkuq4axu2pfs8txb3pw272vties1xpx.png)
2) Right:
![\lim_(x\to3^+)\sin{(\pi)/(\floor[x])](https://img.qammunity.org/2021/formulas/mathematics/high-school/xfu2u9ho6rg3helopho7zw8h3ruqew7dqg.png)
Since we're coming from the right this time, the values are going to be 3.01, 3.001, 3.001.
And, the greatest integer less than or equal to 3.01, 3.001, and 3.001... is 3.
Therefore:
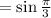
Simplify:
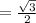
So:
![\lim_(x\to3^+)\sin{(\pi)/(\floor[x])=(\sqrt3)/(2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/yvdijn186wfr99n8wr0crntno8njxivxts.png)
At 3:
So we have:
![\lim_(x\to3)\sin{(\pi)/(\floor[x])](https://img.qammunity.org/2021/formulas/mathematics/high-school/pnxjdzdyvqjbzhphdgag31gcyossjhoryo.png)
The greatest integer of 3 is just 3. So:
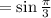
Simplify:
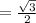
So:
![\lim_(x\to3)\sin{(\pi)/(\floor[x])=(\sqrt3)/(2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/s7njy7ue34la0s7fzbsrelwgjny85j0my1.png)