Question

The sun is 24 degreesabove the horizon. It makes a 51 m long shadow of a tall tree. how talll is the tree

Answer 1

The tree is approximately 22.707 meters tall.

Explanation:

The geometric diagram of the problem is included below as attachment. The height of the tree is found by means of trigonometric functions:

`\tan \alpha = (h)/(w)`

Where:

`\alpha` - Elevation angle, measured in sexagesimal degrees.

`h` - Height of the tree, measured in meters.

`w` - Length of the tree shadow, measured in meters.

The height of the tree is cleared in the equation:

`h = w\cdot \tan \alpha`

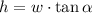
If
`w = 51\,m` and
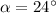`\alpha = 24^(\circ)`, the height is:

`h = (51\,m)\cdot \tan 24^(\circ)`

`h \approx 22.707\m`

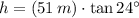
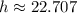
The tree is approximately 22.707 meters tall.