Question

Suppose Stark Ltd. just issued a dividend of $1.59 per share on its common stock. The company paid dividends of $1.25, $1.33, $1.40, and $1.51 per share in the last four years. a. If the stock currently sells for $40, what is your best estimate of the company’s cost of equity capital using the arithmetic average growth rate in dividends? (Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.) a. What if you use the geometric average growth rate? (Do not round intermediate calculations and enter your answer as a percent rounded to 2 decimal places, e.g., 32.16.)

Answer 1

The answer is below

Step-by-step explanation:

a) The dividend growth rate is given as D2/D1 - 1

Year Dividend Growth rate

1 $1.25

2 $1.33 ($1.33/ $1.25 - 1) 6.4%

3 $1.4 ($1.4/$1.33 - 1) 5.26%

4 $1.51 ($1.51/$1.4 -1) 7.86%

The arithmetic average growth rate is the average of all the growth rates.

Arithmetic average growth rate = (6.4% + 5.26% + 7.86%) / 3 = 6.51%

The cost of annuity = (cost of common stock / Selling stock price) * 100% + Average growth rate

The cost of annuity = ($1.59 / $40) * 100% + 6.51% = 10.49%

b) The geometric growth rate is given as:

geometric average growth rate =

`((D_n)/(D_o) )^{(1)/(n) }-1\\D_n=1.51,D_o=1.25,n=3\\\\Geometric\ growth\ rate=(1.51)/(1.25)^(1/3)-1=6.5\%`

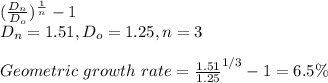
The cost of annuity = ($1.59 / $40) * 100% + 6.5% = 10.48%