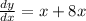Question

Find the indefinite integral and check the result by differentiation. (Use C for the constant of integration.)

∫ (x + 8x) dx

Answer 1

`y = (9x^2)/(2) + c`

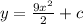
Explanation:

Given

`\int\limits^ _`
`(x + 8x) dx`

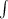
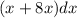
Required

(a) Integrate

(b) Check using differentiation

To integrate, we make use of the following formula;

if

`(dy)/(dx) = \int\limits^{} _{} ax^n`

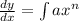
then

`y = (ax^(n+1))/(n+1)`

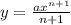
So;
`\int\limits^ _`
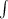
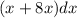`(x + 8x) dx` becomes

`y = (x^(1+1))/(1+1) + (8x^(1+1))/(1+1) + c`

`y = (x^(2))/(2) + (8x^(2))/(2) + c`

`y = (x^(2))/(2) + 4x^2 + c`

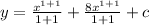
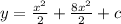
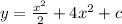
Take LCM

`y = (x^(2) + 8x^2)/(2) + c`

`y = (9x^2)/(2) + c`

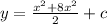
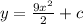
To check using differentiation, we make use of

if
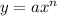`y = ax^n`, then

`(dy)/(dx) = nax^(n-1)`

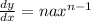
Using this formula

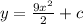`y = (9x^2)/(2) + c` becomes

`(dy)/(dx) = 2 * (9x^(2-1))/(2)`

`(dy)/(dx) = 2 * (9x)/(2)`

`(dy)/(dx) =9x`

`9x = x + 8x`

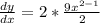
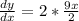
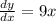
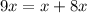
So;

`(dy)/(dx) = x + 8x`