Question

The cost in dollars of making x items is given by the function C(x)=10x+800. a. The fixed cost is determined when zero items are produced. Find the fixed cost for this item. Fixed cost =$ Number b. What is the cost of making 25 items? C(25)=$ Number c. Suppose the maximum cost allowed is $2300. What are the domain and range of the cost function, C(x)? When you enter a number in your answer, do not enter any commas in that number. In other words if you want to enter one thousand, then type in 1000 and not 1,000. It's not possible to understand what the interval (1,000,2,000) means, so you should write that as (1000,2000). Domain: Preview Range: Preview

Answer 1

1. Fixed cost is $800

2.Cost of 25 bags is $1025

3. (170,2300)

Explanation:

Given

`c(x) = 10x + 800`

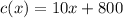
Solving (a): Fixed cost

From the question, fixed cost is when x = 0;

Substitute 0 for x in
`c(x) = 10x + 800`

`c(0) = 10 * 0 + 800`

`c(0) = 0 + 800`

`c(0) = 800`

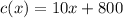
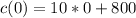
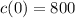
Hence, the fixed cost is $800

Solving (b): Cost of making 25 items

Here; x = 25

Substitute 25 for x in
`c(x) = 10x + 800`

`c(25) = 10 * 25 + 800`

`c(25) = 250 + 800`

`c(25) = 1025`

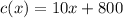
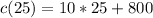
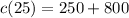
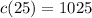
Hence, the cost of 25 bags is $1025

Solving (c): Domain and Range where Maximum cost = $2300

Here; c(x) = 2500

Substitute 25 for c(x) in
`c(x) = 10x + 800`

`2500 = 10x + 800`

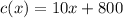
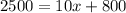
Subtract 800 from both sides

`10x = 2500 - 800`

`10x = 1700`

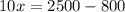
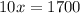
Divide both sides by 10

`x = 170`

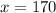
The domain and range of a function is in form of (x,c(x))

Hence, the domain and range is (170,2300)