Answer:
In the long run, ou expect to lose $4 per game
Explanation:
Suppose we play the following game based on tosses of a fair coin. You pay me $10, and I agree to pay you $n^2 if heads comes up first on the nth toss.
Assuming X be the toss on which the first head appears.
then the geometric distribution of X is:
X
 geom(p = 1/2)
geom(p = 1/2)
the probability function P can be computed as:
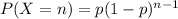
where
n = 1,2,3 ...
If I agree to pay you $n^2 if heads comes up first on the nth toss.
this implies that , you need to be paid
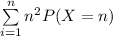
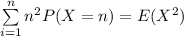
![\sum \limits ^(n)_(i=1) n^2 P(X=n) =Var (X) + [E(X)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/va60gr1otbbn7wwf2iami8w33cp3s2l3gs.png)
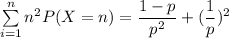 ∵ X
∵ X
 geom(p = 1/2)
geom(p = 1/2)
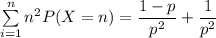
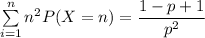
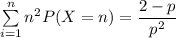

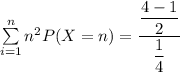

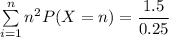
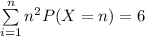
Given that during the game play, You pay me $10 , the calculated expected loss = $10 - $6
= $4
∴
In the long run, you expect to lose $4 per game