Question

The average travel time to work for a person living and working in Kokomo, Indiana is 17 minutes. Suppose the standard deviation of travel time to work is 4.5 minutes and the distribution of travel time is approximately normally distributed. Suppose that it is reported in the news that 8% of the people living and working in Kokomo feel "very satisfied" with their commute time to work. What is the travel time to work that separates the 8% of people with the shortest travel times from the other 92% with longer travel times

Answer 1

The travel time to work that separates the 8% of people with the shortest travel times from the other 92% with longer travel times is 10.6 minutes.

Explanation:

We are given that the average travel time to work for a person living and working in Kokomo, Indiana is 17 minutes.

Suppose the standard deviation of travel time to work is 4.5 minutes and the distribution of travel time is approximately normally distributed.

Let X = the distribution of travel time

The z-score probability distribution for the normal distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = average travel time = 17 minutes

`\sigma` = standard deviation = 4.5 minutes

So, X ~ Normal(
`\mu=17, \sigma^(2) =4.5^(2)`)

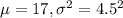Now, we have to find the travel time to work that separates the 8% of people with the shortest travel times from the other 92% with longer travel times, that means;

P(X < x) = 0.08 {where x is the required travel time}

P(
`(X-\mu)/(\sigma)` <
`(x-17)/(4.5)` ) = 0.08

P(Z <
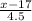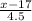`(x-17)/(4.5)` ) = 0.08

In the z table the critical value of z that represents the below 8% of the area is given by -1.43, that is;

`(x-17)/(4.5)=-1.43`

`{x-17}{}=-1.43* 4.5`

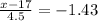
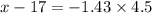
x = 17 - 6.435 = 10.6 minutes

Hence, the travel time to work that separates the 8% of people with the shortest travel times from the other 92% with longer travel times is 10.6 minutes.