Question

Find the value of the linear correlation coefficient r. The paired data below consist of the costs of advertising (in thousands of dollars) and the number of products sold (in thousands):

Cost 9 2 3 4 2 5 9 10
Number 85 52 55 68 67 86 83 73
A.-0.071
B. 0.708
С. 0.235
D. 0.246

Answer 1

(B) 0.708

Explanation:

The table, representing details of this information and all that are necessary to calculate the linear correlation coefficient r, has been attached to this response.

With all details well represented on the table, we can now find the linear correlation coefficient r using the relation attached to this response:

From the relation;

n = sample size = 8

∑xy = 3347

∑x = 44

∑y = 569

∑x² = 320

∑y² = 41681

Substitute these values into the relation as follows;

`r = \frac{3347 - (44* 569)/(8) }{\sqrt{(320 - (44^2)/(8) )(41681 - (569^2)/(8) ) } }`

`r = (217.50)/(307.32)\\`

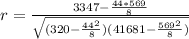
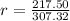
r = 0.7077

r = 0.708 to 3 decimal places

Therefore, the value of the linear correlation coefficient is 0.708