Answer:
(a) The value of P (X = 1, Y = 2) is 0.1583.
(b) The value of P (X + Y = 1) is 0.1055.
Explanation:
It is provided that:
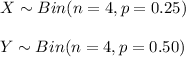
The variables X and Y are independent random variables.
The probability mass function of a Binomial distribution is:
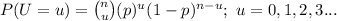
(a)
Compute the value of P (X = 1, Y = 2) as follows:
![P(X=1,Y=2)=[{n\choose x}(p_(x))^(x)(1-p_(x))^(n-x)]* [{n\choose y}(p_(y))^(y)(1-p_(y))^(n-y)]](https://img.qammunity.org/2021/formulas/mathematics/college/r58oqkkf8ua2na72kr4dll8466zxdcb0rw.png) ; Independent
; Independent
![=[{4\choose 1}(0.25)^(1)(1-0.25)^(4-1)]* [{4\choose 2}(0.50)^(2)(1-0.50)^(4-2)]\\\\=0.422* 0.375\\\\=0.15825\\\\\approx 0.1583](https://img.qammunity.org/2021/formulas/mathematics/college/nelw1cspzi6qk47f7mg07vqxqvyyz377sd.png)
Thus, the value of P (X = 1, Y = 2) is 0.1583.
(b)
Compute the value of P (X + Y = 1) as follows:
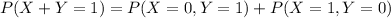
![=\{[{4\choose 0}(0.25)^(0)(1-0.25)^(4-0)]* [{4\choose 1}(0.50)^(1)(1-0.50)^(4-1)]\}\\+\{[{4\choose 1}(0.25)^(1)(1-0.25)^(4-1)]* [{4\choose 0}(0.50)^(0)(1-0.50)^(4-0)]\}\\\\=(0.3164* 0.25)+(0.422*0.0625)\\\\=0.0791+0.0264\\\\=0.1055](https://img.qammunity.org/2021/formulas/mathematics/college/xvngnmowdfx8me4uo3vyjejroxmskaeqcq.png)
Thus, the value of P (X + Y = 1) is 0.1055.