Answer:
r = 2
Explanation:
nth term of a geometric sequence =
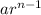 .
.
Where,
a = first term, r = common ratio,
We are given that, the 11th term is 32 times larger than the 6th term of the geometric sequence. Thus:
the 6th term can be expressed as
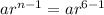

The 11th term is expressed as
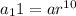
Since the 11th term is 32 times larger than the 6th term, therefore, the following equation can be derived to find the common ratio, r, of the sequence:
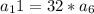
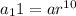
 , therefore:
, therefore:

Divide both sides by ar⁵
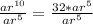
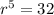

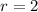
Common ratio = 2