Answer:
The value of fraction of energy is
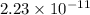
The value of fraction of energy is

Step-by-step explanation:
Given that,
Charge = q
Acceleration = a
The rate at which energy is emitted from an accelerating charge
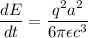 ....(I)
....(I)
We know that,
Acceleration for circular motion is
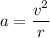 ....(II)
....(II)
The kinetic energy is
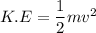
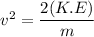
Put the value of v in equation (II)
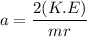
Put the value of a in equation (I)
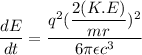
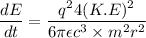
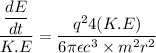
Suppose that,
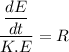
So,
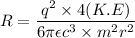 ....(III)
....(III)
(a). For proton,
We need to calculate the fraction of its energy does it radiate per second
Using equation (III)
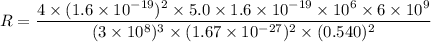
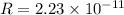
(b). For electron,
We need to calculate the fraction of its energy does it radiate per second
Using equation (III)
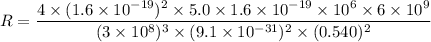
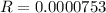
Hence, The value of fraction of energy is
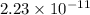
The value of fraction of energy is
