Question

Johnson's Household Products has a division that produces two sizes of bar soap. The demand equations that relate the prices p and q (in dollars per hundred bars), to the quantities demanded, x and y (in units of a hundred), of the 3.5-oz size bar soap and the 5-oz bath size bar soap are given by p = 80 - 0.01x - 0.005y and q = 50 - 0.005x - 0.015y. The fixed cost attributed to the division is exist10,000/week, and the cost for producing 100 3.5-oz size bars and 100 5-oz bath size bars is exist8 and exist12, respectively.

(a) What is the weekly profit function P(x, y)? P(x, y) =
(b) How many of the 3.5-oz size bars and how many of the 5-oz bath size bars should the division produce per week to maximize its profit? 3.5-oz bars 5-oz bars What is the maximum weekly profit?

Answer 1

The weekly profit function P(x,y) = 72x - 0.01x² -0.005xy + 38y - 0.005xy -0.015y² - 10000

3.5 oz bars = 3560

5 oz bars = 80

The maximum weekly profit = 119680

Explanation:

Given that:

the demand functions are p and q

the variable cost of x = 8x and the variable cost of y = 12y

Since the fixed cost attributed to the division is exist 10,000/week

∴ the total cost C = 8x + 12y + 10000

R(x,y) = p(x) + q(y)

where ;

xp(x) = 80x -0.01x² -0.005y

yqz(y) = 50 -0.005x -0.015y²

R(x,y) = 80x -0.01x² -0.005xy + 50y -0.005xy -0.015y²

The weekly profit function P(x,y) = R(x,y) - C

P(x,y) = 80x -0.01x² -0.005xy + 50 -0.005xy -0.015y² - ( 8x + 12y + 10000)

P(x,y) = 80x -0.01x² -0.005xy + 50 - 0.005xy -0.015y² - 8x -12y - 10000

P(x,y) = 72x - 0.01x² -0.005xy + 38y - 0.005xy -0.015y² - 10000

(b) How many of the 3.5-oz size bars and how many of the 5-oz bath size bars should the division produce per week to maximize its profit?

profit will be maximized if:

`(\partial P)/(\partial x) =0 \ and \ (\partial P)/(\partial y) =0`

given that:

`(\partial^2 P)/(\partial x^2) < 0 \ and \ D >0`

where;

D = Px Py -Pxy²

Now;

`(\partial P)/(\partial x) =(-0.02 x -0.01 y +72)`

`(\partial P)/(\partial y) =(-0.03 x -0.01 y +38)`

`(\partial P)/(\partial x) =0 \to 2x+y = 7200`

`(\partial P)/(\partial y) =0 \to x+3y = 3800`

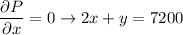
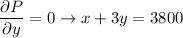
2x + y = 7200

2x + 6y = 7600

5y = 400

y = 400/5

y = 80

From

x + 3y = 3800

x + 3(80) = 3800

x = 3800 - 240

x = 3560

∴ 3.5 oz bars = 3560

5 oz bars = 80

What is the maximum weekly profit?

The maximum weekly profit = 72x - 0.01x² -0.005xy + 38y - 0.005xy -0.015y² - 10000

The maximum weekly profit = 72(3560) - 0.01(3560)² -0.005(3560)(80) + 38(80) - 0.005(3560)(80) -0.015(80)² - 10000

The maximum weekly profit = 256320 - 126736 - 1424 + 3040 - 1424 -96 - 10000

The maximum weekly profit = 119680