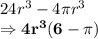Question

Three spherical balls with radius r are contained in a rectangular box. two of the balls are each touching 5 sides of the rectangular box and the middle ball. the middle ball also touches four sides of the rectangular box. What is the volume of the space between the balls and the rectangular box? This is a SAT question and is no calculator. Show all the work Answer is 4r^3(6-pi)

Answer 1

`\bold{4r^3 (6-\pi)}`

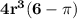
Explanation:

Let us try to visualize the given situation in the form of 2 Dimensional image as shown in the attached diagram.

Let the Diameter of spherical balls be D.

As the spherical balls are completely fit in the rectangular box, the sides of box become:

`D * D* (3 * D)` OR
`D* D* 3D`

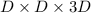
We know that Diameter is twice of radius.

Therefore
`D = 2r`

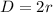
So, the dimensions of rectangular box becomes:

`2r * 2r * 6r`

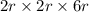
Volume of a rectangular box is given as:

`V = Length * Width * Height\\\Rightarrow V = 2r* 2r* 6r = \bold{24r^3}`

Now, let us find out the volume of each spherical ball.

Volume of a sphere with radius 'r' is given as:

`V_(sphere) = (4)/(3)\pi r^3`

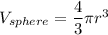
Volume of 3 spheres =
`3* (4)/(3)\pi r^3 =4\pi r^3`

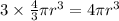
Now, the volume of space between the balls and rectangular box is = Volume of rectangular box - Volume of 3 balls

`24r^3 - 4\pi r^3\\\Rightarrow \bold{4r^3 (6-\pi)}`