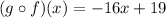Question

Someone help please thank you

Answer 1

See below.

Explanation:

So we have the two functions:

`f(x)=8x-5\text{ and } g(x)=9-2x`

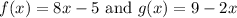
And we want to find:

`(f\circ g)(x)\text{ and } (g\circ f)(x)`

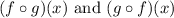
1)

Recall that:

`(f\circ g)(x)`

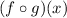
is the same as:

`=f(g(x))`

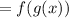
Thus, we can substitute g(x):

`=f(9-2x)`

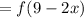
And substitute that into f(x):

`f(x)=8x-5\\f(9-2x)=8(9-2x)-5`

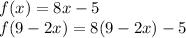
Distribute:

`=72-16x-5`

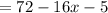
Subtract and simplify:

`=67-16x\\=-16x+67`

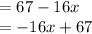
Thus:

`(f\circ g)(x)=-16x+67`

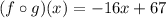
2)

Similarly:

`(g\circ f)(x)=g(f(x))`

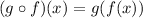
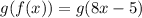
Substitute f(x):

`g(f(x))=g(8x-5)`

Substitute:

`g(8x-5)=9-2(8x-5)`

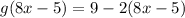
Distribute:

`=9-16x+10`

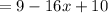
Simplify:

`=-16x+19`

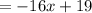
Therefore:

`(g\circ f)(x)=-16x+19`