Question

Q.Solve the following circuit find total resistance RT. Also find value of voltage across resister RC.

Answer 1

R_total = 14.57 Ω , V_C = 1.176 V

Step-by-step explanation:

To solve this circuit we are going to find the equivalent resistance of each branch, let's remember

* Serial resistance

`R_(eq)` = ∑
`R_(i)`

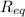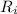
* For resistance in parallel

1 / R_{eq} = ∑ 1/R_{i}

We solve the two branches of the wheatstone bridge

Series resistors

Branch B

R_B = Rb + R4

R_B = 2 + 18

R_B = 20 Ω

Branch C

R_C5 = Rc + R5

R_C5 = 3 + 12

R_C5 = 15 Ω

Resistance in parallel R_B and R_C5

1 / R_BC = 1 / R_B + 1 / R_C5

1 / R_BC = 1/20 + 1/15 = 0.116666

R_BC = 8.57 Ω

Now we have a single branch, we solve the series resistance

R_total = R_A + R_BC

R_total = 6 + 8.57

R_total = 14.57 Ω

b) they ask us for the voltage in the resistance R_C

Let's remember that the voltage in a series circuit is the sum of the voltages

10 = V_a + V_BC

10 = i R_a + i R_BC = i (R_a + R_BC)

i = 10 / (R_a + R_BC)

i = 10 / (14.57)

i = 0.6863 A

The current in the series circuit is constant

V_BC = i R_BC

V_BC = 0.6863 8.57

V_BC = 5.8819 V

This voltage is divided in the bridge, for the two branches in parallel it is the same, but the resistance is different in each branch.

Branch C

V_BC = i R_C5

i = V_BC / R_C5

i = 5.8819 / 15

i = 0.39213 A

In this branch we have two resistors in series, let's remember that the current in a series circuit is constant

V_C = i R_C

V_C = 0.39213 3

V_C = 1.176 V