Question

Solve the problem. A variable x has the possible observations shown below. Possible observations of x: -3 -1 0 1 1 2 4 4 5 Find the z-score corresponding to an observed value of x of 2.

Answer 1

`z = 0.228`

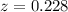
Explanation:

Given

x: -3 -1 0 1 1 2 4 4 5

n = 9

Required

Determine the z-score x = 2

z score is calculated by

`z = (x - Mean)/(SD)`

First, we need to calculate the mean

`Mean = (\sum x)/(n)`

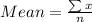
Mean = \frac{-3- 1 + 0 + 1 + 1 + 2 + 4 + 4 +5}{n}

`Mean = (13)/(9)`

`Mean = 1.44`

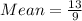
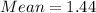
Next is to calculate the standard deviation

`SD = (\sum (x_i - Mean)^2)/(n)`

`SD =\sqrt{ ((-3-1.44)^2+(-1-1.44)^2+(0-1.44)^2+(1-1.44)^2+(1-1.44)^2+(2-1.44)^2+(4-1.44)^2+(4-1.44)^2+(5-1.44)^2)/(9)`
`SD =\sqrt{ ((-4.44)^2+(-2.44)^2+(-1.44)^2+(-0.44)^2+(-0.44)^2+(0.56)^2+(2.56)^2+(2.56)^2+(3.56)^2)/(9)`

`SD =\sqrt{ (19.7136+5.9536+2.0736+0.1936+0.1936+0.3136+6.5536+6.5536+12.6736)/(9)`

`SD =\sqrt{ (54.2224)/(9)`

`SD =√(6.02471111111)`

`SD = 2.455`

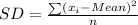
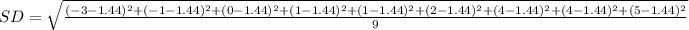
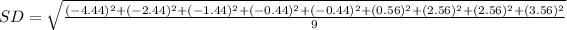
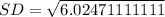
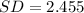
Substitute these values in

`z = (x - Mean)/(SD)`

Where x = 2

`z = (2 - 1.44)/(2.455)`

`z = (0.56)/(2.455)`

`z = 0.228`

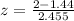
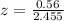
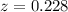
Hence, the z score of x = 2 is o.228