Answer:
Explanation:
A). If a function 'f' is inverse of another function 'g',
Then f[g(x)] = x = g[f(x)]
In this question the given functions are,
f(x) =
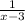 and g(x) =
and g(x) =

Then, f[g(x)] =
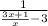
=
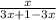
= x
Similarly, g[f(x)] =
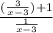
=
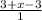
= x
Therefore, Both the functions are inverse of each other.
B). Domain of the compositions of these functions will be a set of all real numbers, (-∞, ∞)