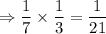Question

You are at a family reunion and the cooler contains ten bottles of soda; four Sprite, three Dr. Pepper, and three Cherry Coke. Three times, you randomly pick up a drink for your grandmother. The first time, you get a Cherry Coke. The second and third times, you get Dr. Pepper. What is the probability of getting Dr. Pepper the fourth time and then an Cherry Coke the fifth time without replacement?

Answer 1

Probability of getting Dr. Pepper the fourth time =
`\frac{1}7`

Probability of getting a cherry coke the fifth time =
`(1)/(3)`

Combined probability =
`(1)/(21)`

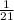
Explanation:

Formula for probability of an event E can be observed as:

`P(E) = \frac{\text{Number of favorable cases}}{\text {Total number of cases}}`

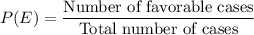
It is given that first time a Cherry coke is chosen and it is not replaced.

So, number of cherry coke left = 2

Dr. Pepper is chosen twice and is not replaced, so

Number of Dr. Pepper left = 3 - 2 = 1

Total number of soda left = 10 - 3 = 7

So, probability of getting Dr. Pepper the fourth time =
`\frac{1}7`

Now, total number of soda left = 7 - 1 = 6

Probability of getting a cherry coke the fifth time =
`(2)/(6) = (1)/(3)`

The combined probability = probability of getting Dr. Pepper the fourth time multiplied with Probability of getting a cherry coke the fifth time

`\Rightarrow \frac{1}7 * (1)/(3) = (1)/(21)`