Answer:
The solution of the inequation
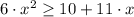 is
is
![\left(-\infty,-(2)/(3)\right]\cup\left[(5)/(2),+\infty\right)](https://img.qammunity.org/2021/formulas/mathematics/college/p9z2yqbrc87ndlfd18t6qoub7nufgcps27.png) .
.
Explanation:
First of all, let simplify and factorize the resulting polynomial:
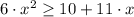
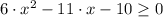

Roots are found by Quadratic Formula:
![r_(1,2) = \frac{\left[-\left(-(11)/(6)\right)\pm \sqrt{\left(-(11)/(6) \right)^(2)-4\cdot (1)\cdot \left(-(10)/(6) \right)} \right]}{2\cdot (1)}](https://img.qammunity.org/2021/formulas/mathematics/college/ehrnfjc6hcksrb427dpyyse6t5uzpi6e8x.png)
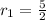 and
and
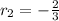
Then, the factorized form of the inequation is:
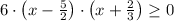
By Real Algebra, there are two condition that fulfill the inequation:
a)


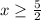
b)
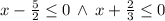
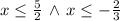
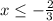
The solution of the inequation
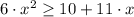 is
is
![\left(-\infty,-(2)/(3)\right]\cup\left[(5)/(2),+\infty\right)](https://img.qammunity.org/2021/formulas/mathematics/college/p9z2yqbrc87ndlfd18t6qoub7nufgcps27.png) .
.