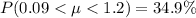Answer:
The percentage is
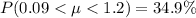
Explanation:
From the question we are told that
The random number is
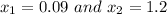
Generally the mean of standard normal distribution is
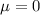
The standard deviation of a standard normal distribution is
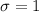
The percentage of the data in a standard normal distribution lies between
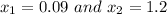 is mathematically represented as
is mathematically represented as
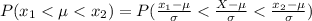
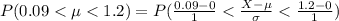
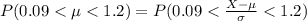
The
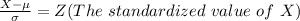
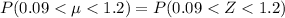
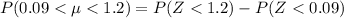
From the z-table
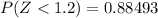
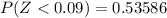
So
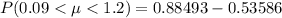
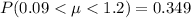
Hence the percentage is