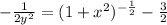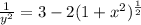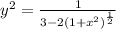Question

Find the solution (in explicit form) for the following initial value problem:    y 0 = xy3 (1 + x 2 ) − 1 2 y(0) = 1.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The solution is
`y^2 = \frac{1}{ 3 - 2 (1 + x^2 ) ^{(1)/(2) }}`

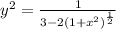
Explanation:

From the question we are told that

The function is
`\left \{ {{y' =  xy^3 (1 + x^2)^{-(1)/(2) }} \atop {y(0) =  1}} \right.`

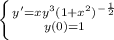
Generally the above equation can be represented as

`(dy)/(dx)  =  xy^3  (1+ x^2)^{- (1)/(2) }`

`=>   (dy)/(y^3)  =  \frac{x}{ (1 + x^2)^{(1)/(2) }} dx`

`\int\limits { (dy )/(y^3) } \,    =  \int\limits {\frac{x}{(1 + x^2) ^{(1)/(2) }} } \, dx`

=>
`- (1)/(2y^2)  =  (1 + x^2)^{(1)/(2) }+ C`

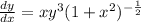
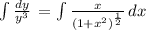
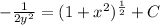
From the question we are told that at y(0) = 1

`- ( 1)/(2 * (1) ) =  (1 + (0)^2)^{(1)/(2) } + C`

`C =  - (3)/(2)`

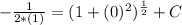
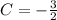
So

`- (1)/(2y^2)  =  (1 + x^2)^{- (1)/(2)}  - (3)/(2)`

`(1)/(y^2)  =  3-2(1 + x^2)^{(1)/(2) }`

`y^2 = \frac{1}{ 3 - 2 (1 + x^2 ) ^{(1)/(2) }}`