Question

For small angles, does the pendulum's period of oscillation depend on initial angular displacement from equilibrium? Explain.

Answer 1

No, the pendulum's period of oscillation does not depend on initial angular displacement.

Step-by-step explanation:

Given that,

For small angle, the pendulum's period of oscillation depend on initial angular displacement from equilibrium.

We know that,

The time period of pendulum is defined as

`T=2\pi\sqrt{(l)/(g)}`

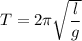
Where, l = length of pendulum

g = acceleration due to gravity

So, The time period of pendulum depends on the length of pendulum and acceleration due to gravity.

It does not depend on the initial angular displacement.

Hence, No, the pendulum's period of oscillation does not depend on initial angular displacement.