Answer:
(B) {6,6,7}
Explanation:
A criterion to determine if each triplet represents a triangle is the Law of Cosine, which states that:

Where
 ,
,
 and
and
 are sides of the triangle and
are sides of the triangle and
 is the angle opposite to side
is the angle opposite to side
 . Now, let is clear the cosine function:
. Now, let is clear the cosine function:
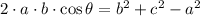
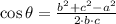
Cosine is a bounded function between -1 and 1, a triplet corresponds to a triangle if and only if result is located between upper and lower bounds. Now let is evaluate each triplet:
a)
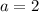 ,
,
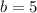 ,
,
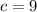

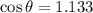 (Absurd)
(Absurd)
The triplet does not represent a triangle.
b)
 ,
,
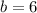 ,
,
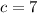

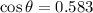 (Reasonable)
(Reasonable)
The triplet represents a triangle.
c)
 ,
,
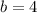 ,
,
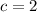

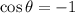 (Absurd)
(Absurd)
The triplet does not represent a triangle, but a straight line.
d)
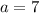 ,
,
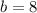 ,
,
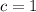
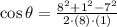
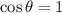 (Absurd)
(Absurd)
The triplet does not represent a triangle, but a straight line.
Hence, the correct answer is B.