Question

Two hoses are filling a pool the first hose fills at a rate of x gallons per minute the second hose fills at a rate of 15 gallons per minute less than the first hose.

Answer 1

B. (0, 5]∪(15,30] only (15,30] contains viable rates for the hoses.

Explanation:

The question is incomplete. Find the complete question in the comment section.

For us to meet the pool maintenance company's schedule, the pool needs to fill at a combined

rate of at least 10 gallons per minute. If the inequality represents the combined rates of the hoses is 1/x+1/x-15≥10 we are to find all solutions to the inequality and identifies which interval(s) contain viable filling rates for the hoses. On simplifying the equation;

`(1)/(x) + (1)/(x-15) \geq (1)/(10)\\\\ find\ the \ LCM \ of \ the function \ on \ the \ LHS\\\\(x-15+x)/(x(x-15)) \geq (1)/(10)\\\\(2x-15)/(x(x-15)) \geq (1)/(10)\\\\10(2x-15)\geq x(x-15)\\\\20x-150\geq x^2-15x\\\\collect \ like \ terms\\-x^2+20x+15x - 150\geq 0\\`

`-x^2+35x-150 \geq 0\\\\multipply \ through \ by \ minus\\x^2-35x+150 \leq 0\\\\(x^2-5x)-(30x+150) \leq 0\\\\x(x-5)-30(x-5) \leq 0\\\\`

`(x-5)(x-30) \leq 0\\\\x-5 \leq 0 and x - 30 \leq 0\\\\x \leq 5 \ and \ x \leq 30`

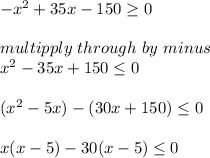
The interval contains all viable rate are values of x that are less than 30. The range of interval is (0, 5]∪(15,30]. Since the pool needs to fill at a combined rate of at least 10 gallons per minute for the pool to meet the company's schedule, this means that the range of value of gallon must be more than 10, hence (15, 30] is the interval that contains the viable rates for the hoses.