Question

Three spherical balls with radius r are contained in a rectangular box. two of the balls are each touching 5 sides of the rectangular box and the middle ball. the middle ball also touches four sides of the rectangular box. What is the volume of the space between the balls and the rectangular box? This is a SAT question and is no calculator. Show all the work Answer is 4r^3(6-pi)

Answer 1

The volume of the space between the balls and the rectangular box is
`4r^(3)(6 - \pi)`

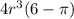
Explanation:

The attachment below shows the description of the rectangular bow and the three spherical balls.

From the description,

• Two of the balls are each touching 5 sides of the rectangular box, say the 5 sides touched by one of the balls are sides 1,2,3,4, and 5; then the other ball will touch sides 2,3,4,5, and 6).
• The middle ball also touches four sides of the rectangular box, These four sides touched by the middle ball will be sides 2,3,4, and 5.

This means the balls are tightly fitted into the rectangular box.

Each of the balls has a radius r

Hence, The volume of one of the balls is given by the volume of a sphere

`Volume of a sphere = (4)/(3) \pi r^(3) \\`

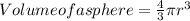
The volume occupied by one of the balls is
`(4)/(3) \pi r^(3) \\`

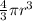
∴ The volume occupied by the three spherical balls will be

3 ×
`(4)/(3) \pi r^(3) \\`

=
`4\pi r^(3)`

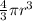
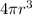
The volume occupied by the three spherical balls
`4\pi r^(3)`

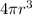
For the rectangular box,

The volume of a rectangular box =
`l w h`

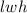
Where
`l\\` is the length

`w` is the width and

`h` is the height

Since the balls are tightly packed,

The width of the rectangular box will be the diameter of the balls

diameter of the balls = 2r

∴
`w` = 2r

The height of the rectangular box will also be the diameter of the balls

∴
`h` = 2r

The length of the rectangular box will be 3 times the diameter of the balls

∴
`l` = 3 × 2r = 6r

Hence,

The volume of a rectangular box = 6r × 2r × 2r

= 24r³

The volume of the space between the balls and the rectangular box is given by

Volume of the space between the balls and the rectangular box =

volume of the rectangular box - volume occupied by the three spherical balls

Volume of the space between the balls and the rectangular box= 24r³ - 4πr³

= 24r³ - 4πr³

= 4r³(6 - π)