Answer:
on [3, 4] = 0.30
on [4, 5] = 0.18
on [5, 6] = 0.12
Explanation:
The average rate of change f, of a function f(x) on an interval [a, b] is given by;
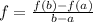-------------(i)
In our case,
f(x) = log 2(3x - 6)
Now let's get the average rate of change of f(x) on;
(i) [3, 4]
Here, a = 3 and b = 4
f(a) = f(3) [This is f(x) at x = 3]
=> f(3) = log[2(3(3) - 6)]
=> f(3) = log[2(9 - 6)]
=> f(3) = log[2(3)]
=> f(3) = log[6]
Also,
f(b) = f(4) [This is f(x) at x = 4]
=> f(4) = log[2(3(4) - 6)]
=> f(4) = log[2(12 - 6)]
=> f(4) = log[2(6)]
=> f(4) = log[12]
Now substitute the values of a, b, f(a) and f(b) into equation (i) as follows;
[Remember that log m - log n = log (m / n)]
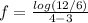
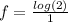
f = log 2 = 0.3010
f = 0.30 [to two decimal places]
∴ The average rate of change on [3, 4] = 0.30
(ii) [4, 5]
Here, a = 4 and b = 5
f(a) = f(4) [This is f(x) at x = 4]
=> f(4) = log[2(3(4) - 6)]
=> f(4) = log[2(12 - 6)]
=> f(4) = log[2(6)]
=> f(4) = log[12]
Also,
f(b) = f(5) [This is f(x) at x = 5]
=> f(5) = log[2(3(5) - 6)]
=> f(5) = log[2(15 - 6)]
=> f(5) = log[2(9)]
=> f(5) = log[18]
Now substitute the values of a, b, f(a) and f(b) into equation (i) as follows;
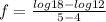[Remember that log m - log n = log (m / n)]
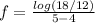
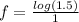
f = log 1.5 = 0.176
f = 0.18 [to two decimal places]
∴ The average rate of change on [4, 5] = 0.18
(iii) [5, 6]
Here, a = 5 and b = 6
f(a) = f(5) [This is f(x) at x = 5]
=> f(5) = log[2(3(5) - 6)]
=> f(5) = log[2(15 - 6)]
=> f(5) = log[2(9)]
=> f(5) = log[18]
Also,
f(b) = f(6) [This is f(x) at x = 6]
=> f(6) = log[2(3(6) - 6)]
=> f(6) = log[2(18 - 6)]
=> f(6) = log[2(12)]
=> f(6) = log[24]
Now substitute the values of a, b, f(a) and f(b) into equation (i) as follows;
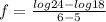[Remember that log m - log n = log (m / n)]
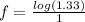
f = log 1.33 = 0.124
f = 0.12 [to two decimal places]
∴ The average rate of change on [5, 6] = 0.12