Answer:
the sphere
Step-by-step explanation:
From the given information,
A free flow body diagrammatic expression for the small uniform disk and a small uniform sphere which are released simultaneously at the top of a high inclined plane can be seen in the image attached below.
From the diagram;
The Normal force mgsinθ - Friction force F = mass m × acceleration a
Meanwhile; the frictional force
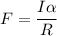
where
 in a rolling motion
in a rolling motion
Then;
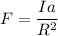
∴
The Normal force mgsinθ - F = m × a can be re-written as:
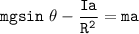
making a the subject of the formula, we have:
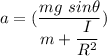
Similarly;
I = mk² in which k is the radius of gyration
∴
replacing I = mk² into the above equation , we have:

where;
the uniform disk
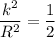
the uniform sphere
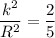
∴
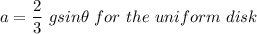

We can now see that the uniform sphere is greater than the disk as such the sphere will reach the bottom first.