Answer:
The value of Cov (X, Y) is 25/6.
Explanation:
It is provided that:

The probability density functions are as follows:
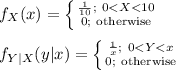
Then the value of f (x, y) will be:
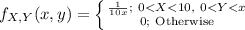
Then f (y) is:
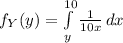
![=(1)/(10)* [\log x]^(10)_(y)\\\\=(1)/(10)[\log 10-\log y]](https://img.qammunity.org/2021/formulas/mathematics/college/h6vef48w3zz4eszyh4yrbdix41td3k7twf.png)
Compute the value of E (X) as follows:
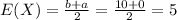
Compute the value of E (Y) as follows:
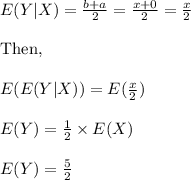
Compute the value of E (XY) as follows:
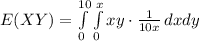
![=\int\limits^(10)_(0)\int\limits^(x)_(0) {(y)/(10)} \, dx dy\\\\=(1)/(10)* \int\limits^(10)_(0){(y^(2))/(2)}|^(x)_(0) \, dx \\\\=(1)/(10)* \int\limits^(10)_(0){(x^(2))/(2)}\, dx\\\\=(1)/(10)* [(x^(3))/(6)]^(10)_(0)\\\\=(100)/(6)\\\\=(50)/(3)](https://img.qammunity.org/2021/formulas/mathematics/college/ec1i5s774pxi1qpzsaww74uzvdwi5vhfug.png)
Compute the value of Cov (X, Y) as follows:
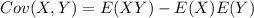
![=(50)/(3)-[5*(5)/(2)]\\\\=(50)/(3)-(25)/(2)\\\\=(100-75)/(6)\\\\=(25)/(6)](https://img.qammunity.org/2021/formulas/mathematics/college/n7b0qj75byns3l2o5e0dfklpt7gowe3pn3.png)
Thus, the value of Cov (X, Y) is 25/6.