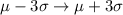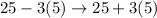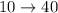Question

a population has a mean of 25 median of 24 and mode of 26 the standard deviation is 5 the value for the

Answer 1

Complete Question

A population has a mean of 25, a median of 24, and a mode of 26. The standard deviation is 5. The value of the 16th percentile is _______. The range for the middle 3 standard deviation is _______.

Answer:

The value of the 16th percentile is
`x = 20`

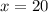
The range for the middle 3 standard deviation is
`10 \to 40`

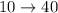
Explanation:

From the question we are told that

The mean is
`\mu  =  25`

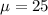
The median is
`m  =  24`

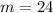
The mode is
`n =  26`

The standard deviation is
`\sigma  =  5`

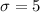
Generally the 16th percentile is mathematically represented as

`P(x)= P((X  -  \mu )/( \sigma )   \le (x- 25 )/(5) ) = 0.16[/te</p><p>Generally  [tex](X -  \mu)/(\sigma )  =  Z(The  \  standardized \  value \ of  \ X  )`

So

`P(x) =  P(Z \le ( x -  25)/(5) ) =  0.16`

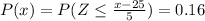
Now from the normal distribution table the z-score of 0.16 is

z = -1

`P(x) =  P(Z \le ( x -  25)/(5) ) =  P(Z \le -1 )`

=>
`(x- 25)/(5)  =  -1`

=>
`x- 25  =  -5`

=>
`x =  25-5`

=>
`x = 20`

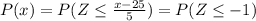
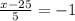
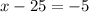
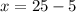
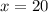
The range for the middle 3 standard deviation is mathematically represented

`\mu  -  3\sigma \to \mu + 3\sigma`

`25 -  3(5 ) \to 25 +  3(5 )`

`10 \to 40`