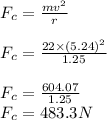Question

A child of mass 22.0 kg is riding a playground merry-go-round that is rotating at 40.0 rev/min. What centripetal force must she experience to stay on if she is 1.25 m from the center

Answer 1

Centripetal Force = 483.3 N

Step-by-step explanation:

A centripetal force is the force that tends to keep a mocing object along a curved path and it is directed towards the centre of the rotatio, while centrifugal force is an apparent force that tends to force a rotating object away from the center of the rotation.

The formula for centripetal force is given by:

`F_c = (mv^2)/(r) \\where:\\F_C = centripetal\ force\\m = mass\ = 22kg\\\omega =angular\ velocity = 40.0\ rev/min`

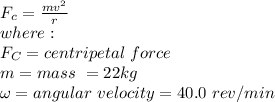
Let us work on the angular velocity (ω), by converting to radians/ seconds

ω = 40 rev/min,

1 rev = 2π rad

∴ 40 rev = 2π × 40 rad = 80π rad

1 min = 60 seconds

`\therefore\ 40\ rev \slash min = (80\ *\ \pi\ rad)/(60\ seconds) \\40\ rev \slash min = 4.189\ rad \slash sec`

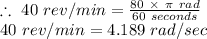
Next let us find the velocity (v) from the angular velocity. Velocity (v) and angulsr velocity (ω) are related by the equation:

v = ω × r (m/s)

v = 4.189 × 1.25

v = 5.24 m/s

Finally, the centripetal force is calculated thus:

`F_c = (mv^2)/(r) \\\\F_c = (22 * (5.24)^2 )/(1.25) \\\\F_c = (604.07)/(1.25)\\ F_c = 483.3N`